멱등성
- 수학적 개념: 연산을 여러번 수행해도 항상 같은 결과를 도출해내는 성질.
- ex) f(f(f(x))) = f(f(x)) = f(x)
함수형 프로그래밍
-
기본 개념: 자료처리를 수학적 함수의 계산으로 취급하고 상태와 가변 데이터를 멀리하는 프로그래밍 패러다임. 프로그래밍이 명령형 프로그래밍의 *문이 아닌 식이나 선언으로 수행되는 선언형 프로그래밍 패러다임을 따르고 있다.
문: 명령형 프로그래밍에서의 가장 작은 독립요소. ex) 대입문, 선언문
명령형의 함수는 수학적 함수와 달리 프로그램의 상태(함수 외부)의 값을 바꿀 수 있는 side effect가 존재한다. 그래서 이러한 함수의 개념을 명확하게 하기 위해 프로시저, 메서드라는 개념이 존재한다.
-
함수형 프로그래밍에 쓰이는 순수 함수: 참조 투명성을 지닌 함수
참조 투명성: 프로그램 동작의 변경없이 관련 값을 대체할 수 있다면 해당 표현식을 참조 투명하다고 한다. 즉, 함수의 결과값이 함수의 인자에만 의존하고 다른 외부의 값에 의존하지 않는 것이다.
그러면 순수 함수는 모두 멱등성의 성질을 지닐까?
개인적으로 생각해봤을 때, 멱등성의 성질을 가지는 함수는 순수함수이지만 순수함수는 모두 멱등성의 성질을 가지는건 아니라고 생각합니다. 즉, 멱등성을 만족하는 함수 ⊆ 순수함수 입니다.
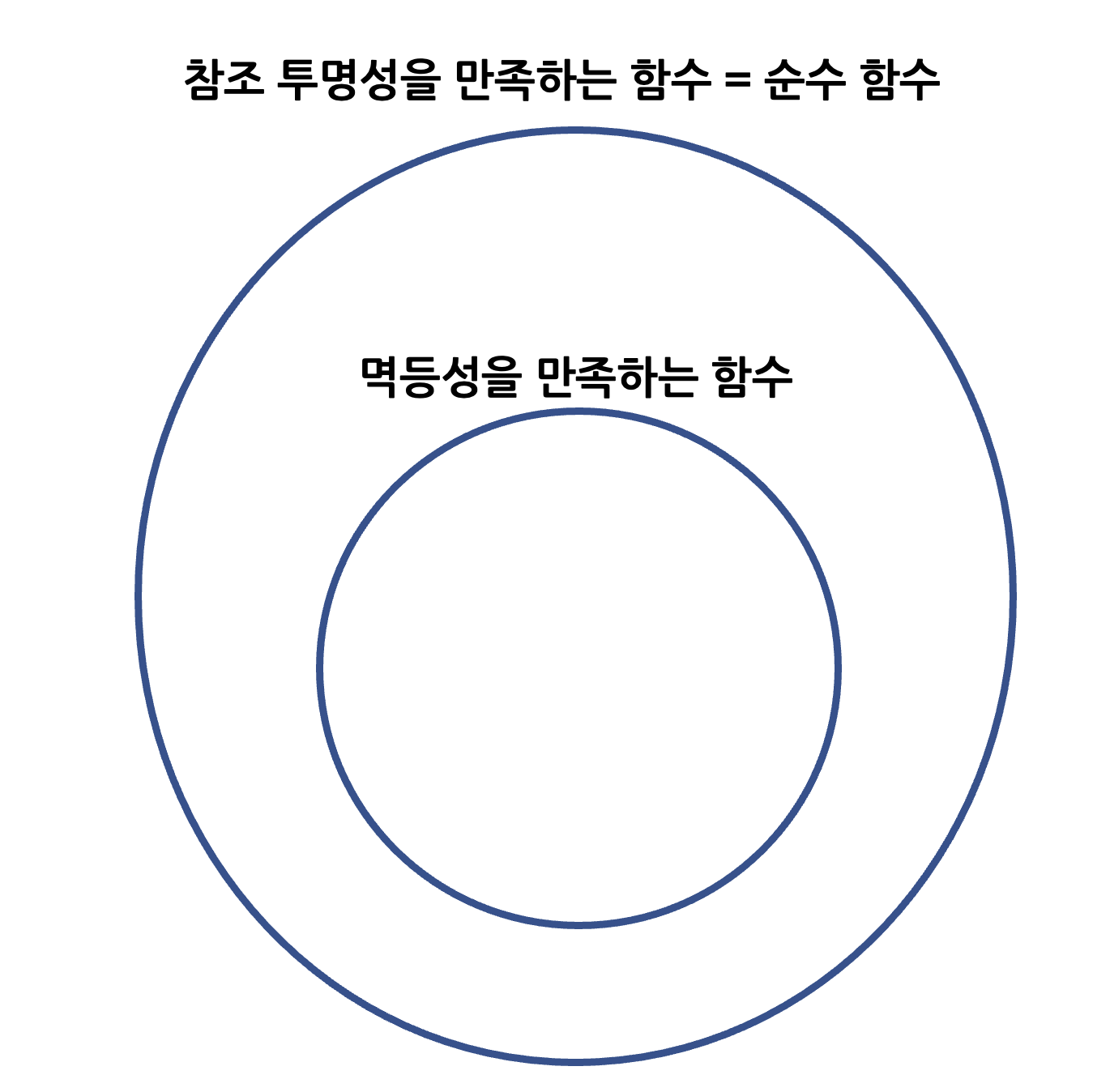
이에 대한 예시로 f(x) = -1*x 의 함수가 있다고 생각해보면, x에 -1을 대입했을 때의 결과는 항상 1이고 외부의 값을 참조하는 것이 아니므로 순수함수에는 성립하지만, f(f(-1)) = -1 이고 f(-1) = 1 이기 때문에 멱등성의 법칙에는 성립하지 않습니다.
AWS 에서는 멱등성을 아래와 같이 설명하고 있습니다.
-> 애플리케이션이나 구성 요소가 반복되는 이벤트를 식별하고 중복, 불일치 또는 데이터 손실을 방지하는 기능.
https://aws.amazon.com/ko/premiumsupport/knowledge-center/lambda-function-idempotent/
해당 문서를 읽어보면 동일한 값에 대한 lambda함수의 실행결과는 항상 같다는 전제하에 식별자를 기반으로 불필요한 반복 실행을 제어하려는 목적을 두고 있습니다.